- v50 information can now be added to pages in the main namespace. v0.47 information can still be found in the DF2014 namespace. See here for more details on the new versioning policy.
- Use this page to report any issues related to the migration.
v0.34:Material science
| This article is about an older version of DF. |
| Material properties |
| Defined: Value • Color • Density • Strain at yield • Temperature values |
| Derived: Magma safety • Fire safety |
| Fluids: Depth • Flow • Pressure |
Materials have a number of properties representing real world variables that describe how they respond to inputs. In particular, the game now has a number of variables that describe what happens to a material when it's put under stress.
What is stress?[edit]
In the real world, an object is stressed when a force is applied to the object. Depending on the nature of the force applied, this stress can take a number of forms, and the object can respond differently based on its material and how that material handles different stresses.
In the material raws, whenever you see 'yield', 'fracture', or 'strain at yield', that property is a stress-related quality.
When does Dwarf Fortress make stress calculations?[edit]
At present, DF seems to only apply forces during combat, and thus only stresses objects (generally armor and various body layers) at that time.
[edit]
The first thing you'll notice is that the second word in each stress variable is one of Yield, Fracture, or strain at yield. These are mechanical performance terms.
The first set of words are things like Impact, Bending, and so forth. These describe modes of applying force.
The following explanations assumes real world physics sort of apply (since Toady One chose real world properties). The game doesn't use all of these properties yet, and may not be applying them according to real world physics.
Mechanical Performance Properties[edit]
Yield: This is almost certainly 'Yield Strength', which is the amount of stress needed to cause a material to go from elastic deformation to plastic deformation. (That is, if you cease stressing the object, does it revert to its original shape or not). Since most objects only elastically deform over small distances of deformation, high Yield values generally means it takes a lot of force to noticeably 'stretch' them (but see strain at yield).
Fracture: The fracture point is the amount of stress or force necessarily to cause the material to fail, or in other words, to break.
Strain at yield (sometimes incorrectly referred to as 'elasticity'): This variable tells you how much deformation occurs to the material while it is deforming elastically. That is, as long as the force is less than the yield strength, stress * strain at yield = deformation distance. The smaller the strain at yield, the less deformation occurs under stress.
Note: Strain at yield is the inverse of the Elastic Modulus. Thus a highly elastic material has low elastic modulus, and engages in less elastic collisions.
Modes of Applying Force[edit]
Impact: Force applied by a sudden strike, like a hammer.
Compressive: Force applied by exerting pressure on an object, like trying to squish something between your hands.
Tensile: Force applied by pulling on something, like suspending one object via another. (e.g., if you suspend an elf from a metal pole, you are applying a tensile force to the pole).
Torsion: Force applied by twisting something. Note that you're twisting some portion of the object relative to itself to cause a torsion stress to be applied to it. (Consider trying to twist a metal rod by grasping at either end and attempting to wring it - yes, you'd have to apply a lot of force to succeed).
Shear: Force applied by pushing part of the material so it tries to slide relative to another part of it. Ie, pushing at the top of an object when the bottom part is fixed to the ground is going to primarily apply a shear stress to it (the top part will try to move in the direction you push, and the lower part will resist this shear stress).
Bending: Force applied by bending a material.
Effects on Combat[edit]
The Dwarf Fortress combat system does not use all material properties at present (0.34.11). Weapon and armor damage/wear/decay is not tracked.
The mechanics governing how material properties impact the protection armor provides against projectiles have been studied reasonably carefully, and are described below. Armor protection from melee weapons has not been studied in detail, although it likely shares many similarities with ranged weapons. Note: all of the below is based on recent (0.34.11) experiments, and many results may be approximate or incomplete.
Projectile Properties[edit]
The main factor determining if a projectile penetrates armor is its momentum. Material properties of the bolt/arrow (except for IMPACT_YIELD, which will be described below), as well as bolt quality and marksdwarf/archer skills do not appear to matter (the skill of the marksdwarf determines if the bolt misses, hits, is dodged, or is blocked with a shield). Dwarven weapons launch projectiles with roughly constant momentum. However rounding of projectile masses can result in some very strange behavior. The complete calculation used to determine projectile momentum is as follows:
- Find the mass of your projectile. Mass=SOLID_DENSITY*SIZE/1,000,000.
- Floor that number to an integer.
- Divide the SHOOT_FORCE of the weapon by the integer, and round the result to the nearest integer.
- Cap the results by the SHOOT_MAXVEL for the weapon.
- Multiply the velocity by the unrounded mass of the projectile to get the momentum.
For DF34.11 values, iron, bronze, copper, silver, and steel bolts/arrows all have mass between 1 and 2, which will be floored to 1, meaning that they will have velocity equal to SHOOT_FORCE (so long as it is less than or equal to SHOOT_MAXVEL). Wood, adamantine, and bone bolts/arrows, as well as all blowdarts, have mass less than 1, and will have velocity which is always equal to SHOOT_MAXVEL and does not depend on SHOOT_FORCE.
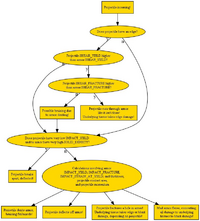
Interactions Between Projectiles and Armor[edit]
When a projectile strikes armor, there are several possible outcomes:
- Conversion of edged damage to blunt damage (chain mail does this).
- The projectile absorbs the force of the collision, and is deflected.
- The armor absorbs all or part of the force of the blow.
- The armor is fractured and does nothing to stop the projectile.
For armor to be at all effective at stopping projectiles, the armor material must have SHEAR_YIELD and/or SHEAR_FRACTURE greater than or equal to the projectile material. Otherwise, the projectile just cuts through the armor like it isn’t there. Additionally, the IMPACT_FRACTURE of the armor must be large relative to the projectile momentum, or the armor fractures and the projectile passes through without slowing down significantly (this happens for metal bolts against any plate armor in 0.34.11).
Conversion of Edged Damage to Blunt Damage[edit]
If the momentum of the projectile is not too high, then chain armor can convert the edged damage normally caused by projectiles to blunt damage, resulting in chips, fractures, jams and bruises, but no tears or cuts. Plate armor does not appear to provide this type of protection under any conditions tested so far. It is not yet known how the momentum needed for edged damage to penetrate chain armor is calculated, but for the cases examined the momentum needed is many times larger than those observed for in-game projectiles.
For a blunt hit, having penetration depth means that it can push fragments of bone into other parts, such as other bone or the brain. If the hit has no fragments, it will break rigid layers (materials with very low strain at yield) and keep going as bruising blunt force, not tearing the body parts underneath. [1]
The Projectile Absorbs the Force of the Collision[edit]
If the projectile does not cut right through the armor (armor material must have SHEAR_YIELD and/or SHEAR_FRACTURE greater than or equal to the projectile material), then it must push in a chunk of the armor. If the armor is not strong enough to resist being pushed in (armor resisting the blow is covered in the next section), then the force to push in the armor is proportional to the mass of the chunk of armor. If the projectile material is not strong enough to exert this force, then it is deformed and deflects. The following algorithm determines if this type of deflection occurs:
- Calculate the volume of armor moved by the projectile. Multiply armor LAYER_SIZE by projectile CONTACT_AREA, and then round down to the nearest 100. If the result is less than 100, then instead round up to 100.
- Mass=armor SOLID_DENSITY times the volume from the last step
- If the IMPACT_YIELD of the projectile is less than mass*(800/157)/PROJECTILE_SIZE, then the projectile deforms and is reported as “deflected”.
In-game, this type of deflection is observed for wood bolts impacting metal armor, and explains why adamantine is observed to be the worst armor for deflecting wood bolts, as it has the lowest density. As explained below, adamantine can barely stop wood bolts using the "Armor Absorbs the Force of the Collision" mechanism, and wood bolts would easily fracture copper or steel armor were it not for the higher densities of those metals causing the projectile to absorb the force of the collision instead.
The Armor Absorbs the Force of the Collision[edit]
This form of deflection depends only on the momentum, but not the material, of the projectile. The armor will provide 50% protection from projectiles if
momentum = (IF-IY/2)*round100(C*S)/(2400000-AU*10000-Q*30000)
where:
- IF is IMPACT_FRACTURE,
- IY is the IMPACT_YIELD of the armor material,
- C is the CONTACT_AREA of the projectile (although it is the smaller of the projectile's contact area and the body part struck's contact area),
- S=LAYER_SIZE of the armor item(s) covering the body part struck,
- AU is the target's armor user skill (0=none, 16=legendary), and
- Q is the armor quality (0=none, 5=masterwork).
- The function round100(x) is equal to 100 if x is less than 100, and 100*floor(x/100) otherwise (rounded down to the nearest 100).
It unclear if or how the thicknesses of multiple armor layers covering one body part stack. This formula is approximate, and the exact values of the coefficients in the denominator may not be accurate. The amount of protection provided drops sigmoidally from 100% to zero over a fairly narrow range. Furthermore, negative status of the target creature (fallen over, unconscious, etc.) are known to significantly reduce armor protection provided. These numbers will roughly predict the results for an ideal, uninjured dwarf, and worse protection should be expected in other cases. The exact manner in which status affects impact armor protection has not yet been explored.
The manner in which armor offers protection is different depending on whether the bolt momentum is greater than 50000/IMPACT_STRAIN_AT_YIELD. If momentum is less than this threshold, then armor can completely deflect projectiles, while if it is larger, armor can significantly slow projectiles so that they cause only bruises (not tears, chips, fractures, or jams).
This type of collision is only observed in-game for bolts with densities less than about 750 (most wood, adamantine) deflecting off adamantine armor. In all other cases the bolt momentum is far to high to be stopped by any armor using this mechanism.